Versuch 1.7

Das Szintillationsspektrometer

1. Grundlagen

Szintillationsspektrometer werden in vielfältiger Weise zum Nachweis und zur Energiebestimmung von radioaktiven Strahlungen benutzt. Die wichtigsten Bestandteile eines Szintillationsspektrometers sind:

1. Szintillator

2. Sekundärelektronenvervielfacher

3. Hochspannungsversorgung

4. Verstärker

5. Differentialdiskriminator

6. Zählgerät

Zur Messung von Gammastrahlung werden vorwiegend NaJ(Tl)-Einkristalle als Szintillatoren verwendet. Natriumjodid- Einkristalle können gut hergestellt werden; die Zugabe von Thallium ermöglicht den Einsatz als Szitillator. Fallen Gammastrahlen in einen derartigen Kristall ein werden durch die bekannten Wechselwirkungsprozesse:

1. Photoeffekt

2. Comtoneffekt

3. Paareffekt

aus den Atomhüllen der Kristallmaterie schnelle Elektronen freigesetzt. Beim Photoeffekt wird die gesamte Energie eines Gammaquants auf ein einzelnes Elektron übertragen. Bei der Abbremsung entsteht im Kristall ein schwacher Lichtblitz, eine sog. „Szintillation“.

Im Meßkopf eines Szintillationsspektrometers, kurz im „Szintillationszähler“, wird der Szintillator auf die lichtempfindliche Photokathode eines „Sekundärelektronenvervielfachers“(SEV) gesetzt. Abbildung 1 zeigt eine Skizze. Die Lichtquanten, die sich im glasklaren Szintillator gut ausbreiten können, gelangen zum Teil auf die Photokathode und bewirken dort die Emission von „Photoelektronen“. Diese werden durch eine angelegte Beschleunigungsspannung zur ersten „Dynode“ hin beschleunigt, die wie die anderen Dynoden auch mit einer Sekundäremissionsschicht belegt ist. Prallt ein Photoelektron auf die Dynode, werden mehrere Sekundärelektronen freigesetzt, die dann zur zweiten Dynode hin beschleunigt werden. Auch dort werden Sekundärelektronen freigesetzt. Bei Verwendung von 10 Dynoden wird die Zahl der ursprünglichen Photoelektronen etwa um den Faktor 10⁶ verstärkt. Jede Szintilation im Kristall ruft damit am Arbeitswiderstand der Anode einen Spannungsimpuls hervor.

Der Szintillaationszähler hat gegenüber dem Geiger-Müller-Zähler einige Voorteile:

1. Die Impulshöhe am Ausgang des Szintillatilonszählers ist proportional der Energie des nachgewiesenen Teilchens.

2. Die Nachweisempfindlichkeit für Gammastrahlung ist gegenübeer dem Geiger-Müller-Zähler erheblich verbessert.

3. Das zeitliche auflösungsvermögen ist ebenfalls wesentlich besser; damit können mit dem Szintillationszähler höhere Impulsraten verarbeitet werden.

Der zuerst genannte Vorteil ermöglicht die Spektroskopie radioaktiver Strahlungen, d.h. die Aufnahme der Intensität der Strahlung als Funktion der Energie. Wir werden uns hier auf die Spektroskopie von Gammastrahlung beschränken, da dies wohl die häufigste Anwendung ist.

Durch die verschiedenen Wechselwirkungsprozesse zwischen einfallender Strahlung und dem Szintillationskristall entstehen -auch bei Einfall exakt monoenergetischer Gammastrahlung- Elektronen verschiedener Energie, die am Arbeitswiderstand entsprechend verschiedene Impulshöhen hervorrufen. Es entsteht ein „Impulshöhenspektrum“. Bei nicht zu komplizierten Srahlenfeldern kann jedoch trotzdem eindeutig auf die Energie der einfallenden Gammastrahlung geschlossen werden.

1.1 Photoeffekt

Beim Photoeffekt wird ein Ekektron aus der Hülle des Getroffenen Atoms Herausgeschlagen. Die gesamte Energie Wg=h*f des Gammaquants wird absorbiert, d.h. das Photon verschwindet und an seiner Stelle tritt das Elektron mit der Kinetischen Energie W_kin,_Ph auf:

W_kin,_Ph = h*f - W_B

W_B ist die Bindungsenergie des Elektrons. Fast alle Photoeffekt - Prozesse finden in den innersten Schalen statt, so daß anschießend charakteristische Röntgenstrahlung emittiert wird. Diese wird jedoch mit großer Wahrscheinlichkeit sofort wieder absorbiert; damit entstehen nach Photoeffekten Impulse, deren Amplitude der gesamten Energie derabsorbierten Gammaquanten entsprechen.

1.2 Comtoneffekt

Unter Comptoneffekt versteht man den elastischen Stoß zwischen einem Photon (Gammaquant) und einem quasifreien Elektron. Abbildung 2 zeigt das Shema eines Comton-Prozesses. Das Gammaquant gibt einen Teil seiner Energie an das Eleltron ab und fliegt mit verminderter Energie weiter. Da sowohl der Energie- als auch der Impulssatz exakt erfüllt ist, kann der Comptoneffekt als Analogon zu einem Billiardkugelstoß gesehen werden. Je nach dem Stzreuwinkel Jist die Energieabgabe mehr oder weniger groß; es gilt für die kinetische Energie des „Comptonelektrons“:

Dabei bedeutet die sog. Reduziete Gammaenergie:

Da der Streuwinkel zwischen 0° und 180° variiert, schwankt die kinetische Energie der Comptonelektronen zwischen:

der Componeffekt führt damit zu erheblichen Komplikationen im Impulshöhenspektrum.

1.3 Paareffekt

Zur Paarbildung muß die Energie eines Gammaquants größer als die doppelte Ruheenergie eines Elektrons sein:

Ist diese Bedingung erfüllt, kann das Gammaquant in ein Elektron-Positron-Paar umgewandelt werden. Dabei geht der Anteil von 1.02 MeV der Gammaenergie in die Ruhemasse des Elektron-Positron-Paares über, der Rest in kinetische Energie des Paares.

Beispiel:

die Auswirkung der drei Effekte auf das Impulshöhenspektrum soll an einem einfachen Beispiel erläutert werden. Es liege eine monoenergetische Gammastrahlung der Energie Wg = 1,5MeV vor. Dann entsteht das in Abb.3 gezeigte schematische Impulshöhenspektrum.

Linie A entspricht dem Photoeffekt, d.h. der Energie Wg=h*f der Gammaquanten. Es kann auch vorkommen, daß zuerst ein Comptoneffekt geschieht und das Streuquant anschließend, noch im Kristall, abermals einen Absorptionsprozeß erleidet. Wird es dabei vollständig absorbiert, so Überlagern sich die beiden Lichtblitze, da sie praktisch gleichzeitig entstehen. Infolgedessen entsteht ein Impuls, der der gesamten Energie des ursprünglichen Gammaquants entspricht und in der „Photolinie“ A registriert wird.

Die Kurve B stellt die Auswirkung des Comptoneffekts dar. Es entsteht eine kontinuierliche Verteilung von der Impuzlshöhe 0 an bis zu einer maximalen Impulshöhe, die der maximalen Energie der Comptonelektronen entspricht. Dort häufen sich die Impulse etwas, da bei Streuwinkeln dei J = 180° (Rückstreuung!) der Winkel nicht stark in W_kin,C eingeht.

Die Linien C und D gehören zu Paareffekten. Die Linie C liegt erwartungsgemäß bei der Energie Wg=1.02MeV; es tritt jedoch noch eine weitere Linie bei Wg=0.51MeV auf. Dies kommt folgendermaßen zustande: Nach einem Paareffekt wird das Elektron-Positron-Paar im Kristall abgebremst; danach zerstrahlt das Positron mit irgendeinem Hjüllenelektron unter Emission von zwei Vernichtungsquanten von je 0,51MeV. Entweichen beide Vernichtungsquanten aus dem Kristall, wird ein Impuls bei der Linie C registriert, entweicht nur eines, wird durch die Absorption des anderen ein Impuls bei der Energie Wg=0.51MeV registriert. Es entsteht die Linie D.

Im realen Impulshöhenspektrum entstehen keine scharfen Linien, sondern mehr oder weniger breite Verteilungen: Sogenannte „Peaks“. Dies ist eine Folge der statistischen Natur der Umsetzung der im Kristall absorbierten Energie in elektrische Impulse. Genauere Untersuchungen haben ergeben, daß die Form der Peaks tatsächlich Gauß’schen Glockenkurven entspricht. Abbildung 4 zeigt eine derartige Kurve. Als „Halbwertsbreite“ eines Peaks wird definiert:

2. Beschreibung der Apparatur.

Zur Aufnahme des Spektrums muß eine Sortierung der Impulse nach Häufigkeit und Impulshöhe vorgenommen werden. Dies geschieht in der einfachsten Form im sog. „Einkanal-Spektrometer“. Abbildung 5 zeigt ein Blockschaltbild.

Zunächst werden die Spannungsimpulse verstärkt und anschließend auf zwei parallel geschaltete Integraldiskriminatoren D1 und D2 gegeben. Dies sind Geräte, die lediglich dann Ausgangsimpulse abgeben, wenn am Eingang die Impulshöhen eine gewisse, einstellbare Schwelle überschreiten. Möchte man z.B. die Impulshäufigkeit zwischen den Impulshöhen U1 und U2 messen, werden die Schwellen der beiden Diuskriminatoren auf U1 und U2 eingestellt. Die Ausgänge werden auf eine Antikoinzidenzschaltung gegeben,die nur dann Ausgangsimpulse liefert, wenn entweder von Diskriminator D1 oder D2 ein Impuls ankommt. Treffen gleichzeitig (etwa innerhalb von 2mSekunden) Impulse von D1 und D2 ein, unterdrückt die Antikoinzidenz die Weiterleitung. Auf diese Weise werden nur die Impulse inm Registriergerät gezählt, deren Amplituden zwischen den Spannungen U1 und U2 liegen; siehe Abbildung 6.

Die beiden Integraldiskriminatoren und die Antikoinzidenzstufe zusammen bilden den sog. „Differentialdiskriminator“, kurz DD. Das Impulshöhenintervall zwischen U1 undU2 wird „Fenster“ oder „Kanal“ genannt. Die Aufnahme des Spektrums erfolgt durch Verschieben des Kanals über die gesamte Impulshöhenverteilung und der Registratur der Impulsraten als Funktion der Kanallage.

Im einfachsten Fall geschieht das Verschieben des Fensters von Hand durch Einstellen eines Präzisions-Dregpotentiometers; meist wird die „Kanalbreite“ starr eingestellt. Besser ausgestattete Gräte verschieben den Kanal selbsttätig, z.B. kontinuierlich und registrieren die Impulsrate mit einem Schreiber. Moderne Geräte, sog. „Vielkanalspektrometer“ besitzen mehrere hundert parallel geschaltete Kanäle und können das Spektrum gleichzeitig aufnehmen.

Neben den schon genannten Bestandteilen eines Szintillationsspektrometers, also Szintillationszählers, Verstärker, Differentialdiskriminator und Registriergerät, gehört zur vollständigen Ausstattung ein Oszillograph. Mit einem Oszillographen kann das Impulshöhenspektrum auf einen Blick übersehen werden und wichtige Parameter wie die Hochspannunggsversorgung des Meßkopfes und die Verstärkung geeignet eingestellt werden.

3. Aufgaben

3.1 Für das Gammastrahlenfeld des Radionuklids Cs-137 ist ein Einkanal-Szintillationsspektrometer passens zu Justieren.

3.2 Das komplette Gammaspektrum dieses Nuklids ist durch Verschieben des Kanals der auf eine konstante Kanalbreite von 1 % des zur Verfügung stehenden Impulshöhenbereichs eingestellt wird, aufzunehmen.

Beispiel: Impulshöhenbereich 2 Volt = 2000mV dann Entspricht die Kanalbreite 20mV.)

3.3 Je nach zur Verfügung stehender Zeit untersuche man folgende Einflüsse:

Einfluß der Kanalbreite auf Lage und Form des Photopeaks.

Einfluß der Zählrate auf Lage und Form eines Photopeaks.

Einfluß von Streumaterial auf ein Gesamtspektrum.

Hinweis: Die Meßwerte trage man sofort in ein Millimeterpapier ein, um das Spektrum sofort überblicken zu können!!! Als Schrittweite wähle man ein Intervall, das der Kanalbreite entspricht.

4. Auswertung

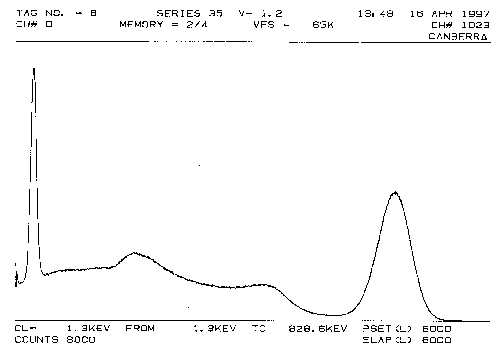
Abbildung 7 zeigt das Impulshöhenspektrum der Gammastrahlung von Cs-137. Dieses Nuklid emittiert monoenergetische Gammastrahlen der Energie Wg = 0,661 MeV.

In ähnlicher Weise stelle man die während der Laborübung aufgenommenen Spektren dar und bestimme bei gut ausgeprägten Photopeaks die Halbwertsbreiten. Man diskutiere die Spektren ausführlich!

5. Fragen

Mit der Formel in Kap. 1.2 für den Comptoneffekt vergleiche man Experiment und Theorie.

Desgleichen mache man sich die Lage des Streupeaks klar. Wie kommt er genau zustande?

Welche Rolle spielt der „Nulleffekt“ bei Spektrometrischen Messungen?

Wann muß u.U. ein „Nullspektrum“ berücksichtigt werden?

6. Literatur

E. Ffünfer und H.Neuert

Zählrohre und Szintillationszähler

G. Baum Verlag, Karlsruhe

K. Fränz

Ein- und Mehrkanal-Impulshöhenanalysatoren

Atompraxis, Jg. 5, Oktober 1959, Heft 10/11

Hinweis: Man überlege sich bei der Vorbereitung des Versuchs zuhause gut den Unterschied bzw. Die Zusammenhänge zwischen dem Bild der Impulse auf einem Oszillographenschirm und dem Impulshöhenspektrum wie in Abb. 7!

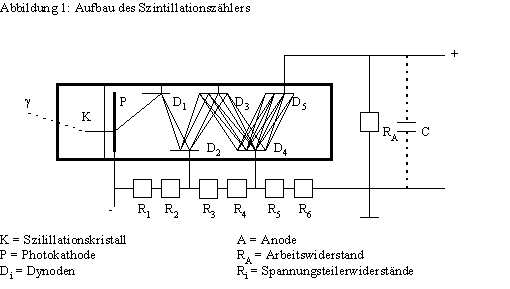
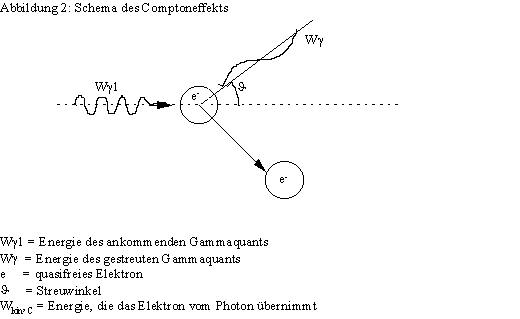
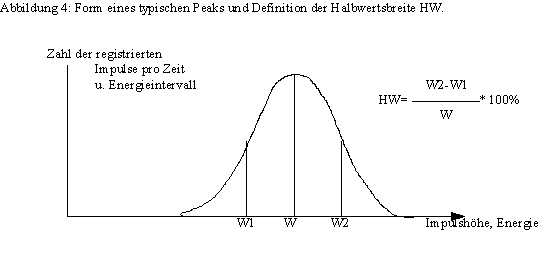
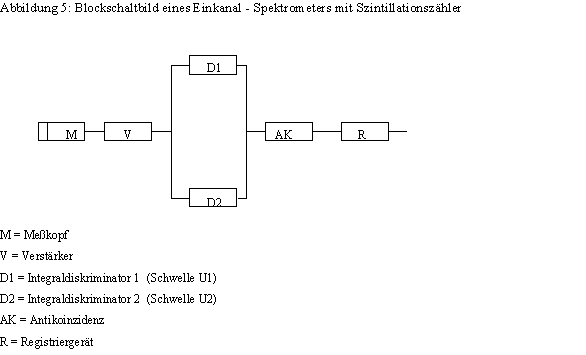
Abbildung 7: Gammaspektrum der momoenergetischen Strahlung von Cs-137

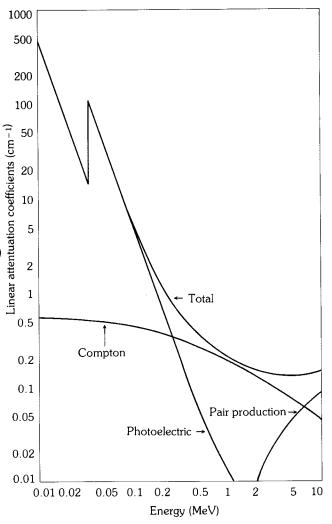
Abbildung 8: Wirkungsquerschnitte für Photo-, Compton- und Paareffekt in NaJ(TL) - Kristallen