VERSUCH 1.13

Messung von nuklidspezifischen Aktivitäten

1. Allgemeines.

Bei einfachen Aufgabenstellungen eignet sich die Gammaspektroskopie mit NaJ(Tl) - Szintillationszählern für nuklidspezifische Aktivitätsbestimmungen. Durch die hohe Dichte der NaJ - Kristalle, die relativ hohe Ordnungszahl von Jod und die Möglichkeit preiswerte großvolumige NaJ - Kristalle herzustellen ist es möglich, Gammastrahlungen sehr effektiv nachzuweisen. Sind die Gammaspektren nicht zu komplex, gestattet die Analyse einzelner gut aufgelöster Gesamtabsorptionslinien (Peaks) den qualitativen und quantitativen Nachweis von Radionukliden. Dazu ist es neben einer Energiekalibrierung nötig, die Nachweiswahrscheinlichkeit des verwendeten Szintillationszählers für Gammastrahlungen als Funktion der Energie zu kennen.

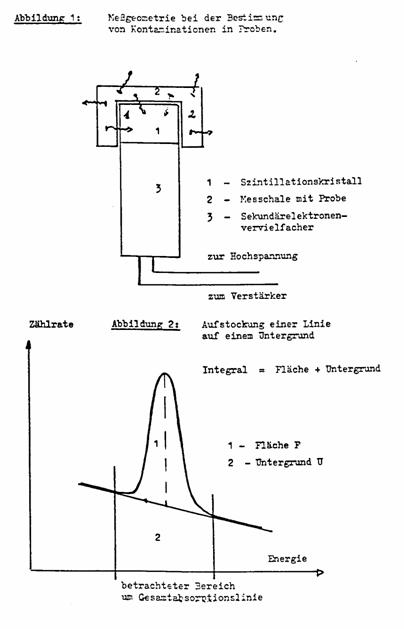
Unter Nachweiswahrscheinlichkeit versteht man hierbei die Wahrscheinlichkeit, mit der die von einer Strahlenquelle in der Nähe des Detektors emmittierten Photonen im Detektor bzw. im Strahlenmeßsystem einen Impuls in der Gesamtabsorptionslinie hervorrufen. Meist werden die Proben in bestimmter, für die Erhöhung der Nachweiswahrscheinlichkeit günstiger Geometrie untersucht. Häufig verwendet wird die Ringschalengeometrie, bei der die Proben in Ringschalen (Inhalt 250 bis 1000 Milliliter) gefüllt werden, die dann über die zylinderförmigen Szintillationskristalle gestülpt werden, siehe Abb. 1.

Zur Kalibrierung hinsichtlich der Nachweiswahrscheinlichkeit werden von der Physikalisch Technischen Bundesanstalt in Braunschweig wässerige Lösungen von Radionukliden mit genau bekanntem Aktivitätsgehalt vertrieben. Die Lösungen enthalten einige Nuklide, deren Emmissionslinien etwa gleichmäßig über den normalen Energiebereich von ca. 100 KeV bis 2 MeV verstreut liegen. Hiermit kann die Nachweiswahrscheinlichkeit als Funktion der Energie bestimmt werden. In manchen Fällen, z.B. zum Nachweis eines einzelnen Nuklids genügt die Kenntnis einer einzigen Nachweiswahrscheinlichkeit bei einer bestimmten Energie. Für diese Fälle stehen auch Kalibrierlösungen mit einem einzigen Radionuklid zur Verfügung.

In manchen Fällen und bei dem vorliegenden Versuch sollen (nahezu) punktförmige Strahlenquellen hinsichtlich der Aktivität betsimmt werden. Es ist hierbei nötig, die Nachweiswahrscheinlichkeiten mit entsprechenden punktförmigen Kalibrierstrahlern zu ermitteln. Natürlich ist die Nachweiswahrscheinlichkeit in diesen Fällen eine Funktion des Abstandes zwischen Detektor und Strahlenquelle.

Die Nachweiswahrscheinlichkeit nimmt mit steigender Energie stark ab. Bei relativ niedrigen Energien können je nach Kristallgröße und -form Nachweiswahrscheinlichkeiten von 20 bis fast 100 % erreicht werden, bei hohen Energien bei ca. 1 MeV bis zu 20 % Prozent.

2. Theoretische Grundlagen.

Der Zusammenhang zwischen der Zählrate in der Gesamtabsorptionslinie eines Gammastrahlers, der Aktivität der Strahlenquelle, der Emmissionswahrscheinlichkeit der betrachteten Gammastrahlung und der Nachweiswahrscheinlichkeit NWW ergibt sich wie folgt:

Aus dieser Gleichung wird üblicherweise mit Hilfe eines Kalibrierstrahlers bekannter Aktivität und bekannter Emmissionswahrscheinlichkeit über die Messung der Zählrate die Nachweiswahrscheinlichkeit bestimmt. In der Praxis wird jedoch meist für eine bestimmte Messzeit t die Zahl der Impulse Z in der Gesamtabsorptionslinie bestimmt. Aus obiger Gleichung ergibt sich dann:

Bei der Ermittlung der Zahl der Impulse in der Gesamtabsorptionslinie muss fast immer ein störender Untergrund berücksichtigt werden, der von der Umgebungsstrahlung und/oder Comptonverteilungen höherenergetischer Linien herrührt. Die ist nicht nur bei der Bestimmung der Nachweiswahrscheinlichkeit, sondern auch bei der Messung unbekannter Aktivitäten wichtig.

Abbildung 2 zeigt die grundsätzliche Aufstockung einer Linie auf einen Untergrund. Meist genügt es, den Untergrund U als Funktion der Energie näherungsweise mit einer linearen Funktion anzunähern. Die Nettozahl von Impulsen in der Linie (Fläche F) ergibt sich dann als Differenz der Gesamtzahl der Impulse im betrachteten Energiebereich (Integral I) minus der Impulszahl im trapezförmigen Untergrund. Als Maß für die Güte der Linie wird oft das Linienkriterium LK angegeben:

Die Statistische Schwankung des Untergrunds SU wird mit der Wurzel aus der Impulszahl im Untergrund - Trapez bestimmt. Bei gut definierten Linien sind die Werte für LK größer als 3.

Der Wert für die Nachweiswahrscheinlichkeit hängt nicht nur stark von der Energie der Strahlung, sondern auch von der Geometrie der Anordnung Strahlenquelle - Detektor ab. Natürlich sinkt die NWW bei zunehmender Entfernung der Strahlenquelle vom Detektor ab. Bei der Versuchsdurchführung achte man daher sehr sorgfältig auf gleiche Messgeometrien beim Kalibrieren und bei der eigentlichen Aktivitätsbestimmung.

Bei Radionukliden, die mehrere Emmissionslinien aufweisen, müssen sehr oft zur genauen Aktivitätsbestimmung Summationskorrekturen berücksichtigt werden. Werden zwei Photonen in einer Kaskade praktisch gleichzeitig emittiert, kann es mit merklicher Wahrscheinlichkeit zur gleichzeitigen Registrierung dieser zwei Photonen kommen, so dass ein Impuls bei der Summe der Einzelenergien auftritt. Aus Gründen der Einfachheit werden diese Effekte hier nicht berücksichtigt.

Eigenschaften der Gaußschen Glockenkurve:

Die bekannte Gaußsche Glockenkurve hat die Gleichung:

wobei die Größen bedeuten:

Ymax = Maximalwert

m = Mittelwert

s = Standardabweichung.

Aus dieser Gleichung können folgende Beziehungen abgeleitet werden:

Halbwertsbreite = 2,335 _* s

Zehntelwertsbreite = 4,292 _* s

Hundertstelwertbreite = 6,070 _* s

Tausendstelwertbreite = 7,434 _* s

Mittelwert +/- 0.5 Halbwertsbreite ca. 76 % der Fläche

Mittelwert +/- 0.5 Zehntelwertsbreite ca. 97 % der Fläche

Mittelwert +/- 0.5 Hundertstelwertbreite ca. 99.7 % der Fläche

Mittelwert +/- 0.5 Tausendstelwertbreite ca. 99.98 % der Fläche

Die Gesamtfläche kann mit Hilfe der Beziehung

Gesamtfläche = 2.5506 _* s _* Ymax

berechnet werden.

3. Aufgabenstellung.

Die Aktivität punktförmiger Strahlenquellen ist durch Vergleich mit entsprechenden Kalibrierstrahlern zu bestimmen. Dabei werden zunächst die Nachweiswahrscheinlichkeiten (mit Fehler) und die Linienkriterien bestimmt. Je nach Zeit sollten mindestens zwei Messungen bei verschiedenen Energien durchgeführt werden.

3.1 Bestimmung der Nachweiswahrscheinlichkeit.

Bei bekannter Energiekalibrierung wird der Bereich um die Gesamtabsorptionslinie eines Kalibrierstrahlers genau vermessen, um die Nachweiswahrscheinlichkeit zu bestimmen.

3.2 Bestimmung unbekannter Aktivitäten.

Anschließend sind in gleicher Geometrie unbekannte Aktivitäten desselben Radionuklids zu bestimmen.

3.3 Überprüfung bei Vorhandensein eines Störstrahlers.

Um die bei 3.1 und 3.2 ermittelten Werte zu überprüfen, werden dieselben Messungen bei Vorhandensein eines höherenergetischen Störstrahlers nochmals ermittelt. Sowohl Nachweiswahrscheinlichkeit als auch die Bestimmung der unbekannten Aktivitäten sollten davon kaum beeinflusst werden, jedoch die Linienkriterien und die Fehler.

4. Durchführung.

Es werden die Szintillationsspektrometer (Versuch 1.7/1.8/1.9) benutzt. Zur Kalibrierung stehen Nuklide zur Verfügung, die Emissionslinien mit genau bekannter Energie und Emissionswahrscheinlichkeit aufweisen, z.B. Am-241, Cs-137 und Co-60.

Nuklid	Gammaenergie keV	Emissionswahr- scheinlichkeit p	Linearer Schwächungskoeffizient
Americium-241	59.5	0.3590	22.00 1/cm
Cäsium-137	661.6	0.8512	0.28 1/cm
Cobalt-60	1173.2 1332.5	0.9990 0.9998	0.19 1/cm 0.18 1/cm

Zur Bestimmung der Nachweiswahrscheinlichkeit werden die Gesamtabsorptionslinien der Kalibrierstrahler genau vermessen. Dazu bringt man die Strahlenquellen in möglichst genau reproduzierbare Lagen zum Detektor. (Die Strahlenenergie und die Geometrie, d.h. der Abstand zwischen Quelle und Detektor bestimmen die Nachweiswahrscheinlichkeit!) Dann wird die Verstärkung des Spektrometers so eingestellt, daß die Gesamtabsorptionslinie zur Ausmessung gut geeignet ist, d.h. weder zu schmal noch zu breit. Der gesamte Bereich einer Linie vom linken Fuß über das Maximum zum rechten Fuß sollte mit etwa 15 bis 20 Messungen lückenlos erfaßt werden. Dazu muß die Schrittweite der nacheinanderfolgenden Messungen genau der eingestellten Kanalbreite entsprechen! Man sagt: Der Bereich der Gesamtabsorptionslinie wird durch ca. 20 Kanäle erfaßt.

Da die Gesamtabsorptionslinien Gaußschen Glockenkurven entsprechen, kann man aus der Gleichung der Glockenkurve ableiten, daß im Bereich

Gammaenergie +/- 0.5 Halbwertsbreite ca. 76% der Impulse

Gammaenergie +/- 0.5 Zehntelwertsbreite ca. 97% der Impulse

Gammaenergie +/- 0.5 Hundertstelwertbreite ca. 99.7% der Impulse

Gammaenergie +/- 0.5 Tausendstelwertbreite ca. 99.98% der Impulse

liegen. Die Erfassung des Energiebereichs von Gammaenergie +/- einer halben Tausendstelwertbreite reicht also aus, die Nachweiswahrscheinlichkeit genügend genau zu bestimmen.

Beispiel:

Die Halbwertsbreite der Linie bei Cs-137 liegt z.B. bei 8 Prozent. Da die Tausendstelwertbreite um einen Faktor 3,15 größer ist, muss bei Cäsium-137 im Bereich 661,6 KeV +/- 0.5 3.15 0.08 661.6 KeV gemessen werden, also bei

661.6 KeV +/- 83.3 KeV

oder von etwa 580 KeV bis 740 KeV. Ist der Messbereich des Spektrometers (0 bis 100 Prozent) derart eingestellt, dass 100% der Energie 1000 KeV entsprechen, muss also von ca. 58% bis ca. 74% gemessen werden. Dies ergibt bei der Kanalbreite von 1% (oder absolut 10 KeV) 16 Messungen. Wird die Verstärkung höher gestellt,. so dass ca. 800 KeV der Messbereichsgrenze von 100% entsprechen, überdeckt die Linie den Bereich von 72% bis 92%, erfordert also 20 Messungen. Hinweis: Kann bei einem Spektrometer die Kanalbreite minimal auf 2% eingestellt werden, ist die Linie unbedingt entsprechend dem Beispiel in den oberen Teil des Messbereichs zu verschieben.

Nach der Aufnahme der Linie des Kalibrierstrahlers wird das Präparat mit der unbekannten Aktivität möglichst genau an den Platz des Kalibrierstahlers gebracht und entsprechend verfahren. Bei großen Aktivitätsunterschieden ist es möglich, dass sich die Lage der Linie leicht verschiebt, da die Impulshöhen von Szintillationsspektrometern etwas von der gesamten verarbeiteten Zählrate abhängig sind. Bei wesentlich kleineren Zählraten muss u.U. die Messzeit pro Messpunkt verlängert werden.

5. Auswertung.

5.1 Die Größen Integral, Fläche und Untergrund werden wie folgt bestimmt: Das Integral I wird als Summe der Impulse über alle Kanäle im gemessenem Bereich der Linie berechnet. Der Untergrund U wird durch ein Trapez angenähert, und die Fläche F aus der Differenz Integral minus Untergrund.

Die Nachweiswahrscheinlichkeit NWW wird somit berechnet nach der Gleichung

Man führe eine Fehlerrechnung durch unter der Annahme, dass die Aktivität A einen relativen Fehler von 2% aufweist, während die Fehler von p und t vernachlässigt werden können. Von merklichem Einfluss sind die statistischen Fehler von I und U.

Hinweis: Es ist hier nicht nötig, für die den Untergrund annähernde Gerade eine Regressionsanalyse durchzuführen.

5.2 Oft liegen die Nachweiswahrscheinlichkeiten je nach Kristallgröße und Entfernung Strahlenquelle - Detektor nur bei einigen Prozenten. Dies ist eine Folge der Tatsache, dass einmal schon bei einem Abstand von einigen Zentimetern zwischen Quelle und Detektor die meisten Photonen den Kristall nicht erreichen, zum andern bei höheren Strahlenenergien viele Photonen den Kristall durchdringen oder nur einen Teil ihrer Energie im Kristall abgeben (Comptonverteilung!). Man schätze für die gegebene Versuchsdurchführung ab, welchen Einfluß die Geometrie bringt und wie viele Photonen den Kristall ohne Wechselwirkung durchdringen. Kristalldurchmesser und - dicke erfragen! Die Wahrscheinlichkeit einer Wechselwirkung im Kristall kann mit dem exponentiellen Schwächungsgesetz und dem totalen linearen Schwächungskoeffizienten von NaJ(Tl) berechnet werden.

5.3 Zum Vergleich berechne man die Fläche F aus der Formel für die Standardabweichung s und dem Maximum ymax.

5.4 Bei der Bestimmung der unbekannten Aktivität benutze man für die Fehlerfortpflanzung den in 4.1 errechneten Fehler der Nachweiswahrscheinlichkeit. Man schätze einen systematischen Fehler ab, der die möglicherweise nicht exakt gleichen Abstände zwischen Kalibrierstrahler sowie unbekannten Strahler und Detektor berücksichtigt.

6. Fragen:

1. Warum wird die Aktivitätsbestimmung durch die möglicherweise zwischen einem starken Kalibrierstrahler und einem schwachen Meßstrahler vorhandene geringe Lageverschiebung der Gesamtabsorptionslinien nicht wesentlich beeinflußt.

2. Wie beeinflußt ein starker Untergrund, z.B. durch einen Störstrahler, die Bestimmung unbekannter Aktivitäten.

3. Wie könnte man mit NaJ(Tl)Szintillationszählern die Nachweiswahrscheinlichkeiten erhöhen?