Physiklabor

Hinweise für die Anfertigung der Versuchsberichte

Bestimmung von

Messwert und Unsicherheit

nach DIN 1319-3

von

Ulrich Schrewe

WS 2002/03

Inhalt:

1. Vorbemerkungen

2. Bestimmung einzelner Messgrößen

2.1 Mittelwert, Standardabweichung, Standardunsicherheit

2.2 Anwendung der Definitionen am Beispiel Längenmessung

2.3 Darstellung der Messwertverteilung

2.4 Relative Unsicherheit, erweiterte Unsicherheit, Vertrauensbereich

2.5 Das vollständig Messergebnis

2.6 Systematische Unsicherheiten

3. Auswerteverfahren bei mehreren Eingangsgrößen

3.1 Korrelationen

3.2 Allgemeines verfahren

3.3 Verfahren bei unkorrelierten Eingangsgrößen

3.4 Regel zur Vereinfachung der Unsicherheitsermittlung

3.5 Anwendungsbeispiele

4. Zusammenfassung

1. Vorbemerkungen

Bei der Anfertigung der Versuchsberichte sind einschlägige Normen und Richtlinien (z. B. DIN) zu beachten. Wichtig ist die DIN 1319: "Grundlagen der Messtechnik", insbesondere der Teil 3: "Auswertung von Messungen einer einzelnen Messgröße; Messunsicherheit". Die Neufassung des Jahres 1996, die eine ältere Version aus dem Jahr 1983 ersetzt, basiert auf Empfehlungen des "Guide to the Expression of Uncertainty in Measurements", abgekürzt "GUM", der "ISO International Organization for Standardization" aus dem Jahr 1993. Gegenüber früheren Darstellungen (die z. B. auch noch in Lehrbüchern zu finden sind), wird im GUM eine etwas geänderte Terminologie und Philosophie zur der Ermittlung von Messunsicherheiten empfohlen. Dies bedeutet keineswegs, dass alle mathematischen Beziehungen in älteren Anleitungen "überholt" sind. Bei der Erstellung neuer Versuchprotokolle ist es aber empfehlenswert, von Anfang an den aktuellen DIN und GUM Richtlinien zu folgen.

Neue Terminologie: Die ältere Literatur verwendete Begriffe wie Messfehler, Fehlerrechnung, Fehlerfortpflanzung, usw. Im Zusammenhang mit Messvorgängen ist der Begriff Fehler jedoch problematisch, denn das allgemeine Sprachverständnis assoziiert mit dem Begriff Fehler, dass etwas falsch ist. Das Abweichen eines Messergebnisses vom wahren Wert einer Messgröße, bedeutet aber nicht, dass die Messung falsch war. Sie wird vielmehr durch die Tatsache verursacht, dass jeder Messvorgang mit einer gewissen Unsicherheit behaftet ist. In Anlehnung an die englischen Begriffe "error" und "uncertainty" verwendet man neuerdings die entsprechenden deutschen Begriffe "Fehler" und "Unsicherheit". Fehler sollte dann verwendet werden, wenn bei einer Messung etwas tatsächlich falsch gemacht worden ist (z. B. wenn bei einer Längenmessung ein ungeeigneter Maßstab verwendet wurde, oder wenn bei der Messung einer elektrischen Größe eine falsche Messgeräteeinstellung gewählt wurde.) Normale nicht-falsche Messungen besitzen immer eine gewisse Unsicherheit, die bei mehreren Einzelmessungen zu einer Streuung der Messdaten führt. Das Messergebnis sollte immer zusammen mit einer Unsicherheit angegeben werden, um die Qualität eines Messverfahrens zu charakterisieren. In der DIN 1319-3 wird die Standard(mess)unsicherheit definiert, die als ein "Kennwert" der Messung angesehen, und als quantitatives Maß für die Unkenntnis der Messgröße angesehen werden kann. Sie kennzeichnet einen Bereich, den man "vernünftigerweise dem wahren Wert der Messgröße als Schätzwert zuweisen kann" (Beachten Sie die sehr allgemeine Definition und die Bezeichnung "Kennwert". Das Messergebnis und die Standard(mess)unsicherheit definieren zwar einen Wertebereich, der für den wahren Wert kennzeichnend ist, aber dieser Bereich hat eine andere Bedeutung als die Vertrauensbereiche, die den wahren Wert mit einer gewissen vorgegebenen Wahrscheinlichkeit, dem Vertrauensniveau, enthalten.) Nach DIN 1319-3 kann man alternativ zur Standard(mess)unsicherheit eine erweiterte Messunsicherheit angeben. In diesem Fall ist aber zwingend gefordert, dass der gewählte Erweiterungsfaktor zusammen mit dem Ergebnis angegeben wird. Zusätzlich (nicht alternativ!) zur Standard(mess)unsicherheit oder erweiterten Messunsicherheit kann ein Vertrauensbereich angegeben werden. Diese Angabe ist besonders bei technischen Mess- oder Kontrollvorgängen sinnvoll. Bei der Bestimmung von physikalischen Größen und Stoffkonstanten aber entbehrlich. Falls eine Angabe zum Vertrauensbereiches gemacht wird, muss in jedem Fall auch das zugehörige Vertrauensniveau mitgeteilt werden.

Ein vollständiges Messergebnis besteht immer aus:

Messwert und (Standard- oder erweiterte ) Messunsicherheit.

Als zusätzlich Angaben sind möglich:

Vertrauensbereich zusammen mit Vertrauensniveau

Messunsicherheiten müssen deutlich von Messabweichungen unterschieden werden. Eine Abweichung bezeichnet die Differenz zweier Werte, z. B die Differenz zwischen den Einzelmessungen und dem Ergebnis einer Messreihe, dem Messwert, oder zwischen dem Messwert und dem wahren Wert der Messgröße (den man ja oft gar nicht kennt). Messunsicherheiten beschreiben aber nicht, wie weit der Messwert vom wahren Wert abweicht, vielmehr kann man (beim Vorliegen bestimmter Voraussetzungen) mit Hilfe der Messunsicherheit eine Wahrscheinlichkeit für das Vorhandensein einer Abweichung zwischen Messwert und wahrem Wert ableiten.

Die Begriffe Fehler und Abweichung sollten nicht dann verwendet werden, wenn eigentlich eine Messunsicherheit gemeint ist.

(Beispiele: Nicht Messfehler, sondern Messunsicherheit, nicht Standardfehler sondern Standardmessunsicherheit.)

(Zusatz: Bei der Durchsicht einer großen Zahl von Versuchsprotokollen zeigte sich, dass ca. 50% der Studenten statt "Standard-" die Schreibweise "Standart-" bevorzugen. Trotz dieses respektablen Abstimmungsergebnisses ist nicht das "t", sondern ein "d" Rechtschreibungsstandard.)

2. Bestimmung einzelner Messgrößen

2.1 Mittelwert, Standardabweichung, Standardunsicherheit

Das Auswerteverfahren für eine einzelne Messgröße und die in der neuen DIN Norm verwendeten Begriffe (gelb unterlegt) sollen am Beispiel einer Längenmessung (Beispiel A.1: der DIN 1319-3) erläutert werden:

Ein Endmaß mit einer Länge von 150,000 mm soll mit einem Längenmessgerät geprüft werden. Die physikalische Größe Y, der die Messung gilt, genannt Messgröße (Ergebnisgröße) ist die Länge L, Y = L. Als wahren Wert der Endmaßlänge betrachte man den angegeben Wert: Y = L = 150,000 mm. Das Ziel jeder Messung ist es, ein Ergebnis zu gewinnen, das dem wahren Wert Y der Messgröße möglichst nahe kommt. Man verwendet Messgeräte, auch Messeinrichtungen genannt, die auf einem bestimmten Messverfahren basieren, das auf das Meßobjekt (hier: das Endmaß) angewendet wird.

Im vorliegenden Beispiel soll das Längenmessgerät sorgfältig kalibriert sein und in dem relevanten Messbereich eine bekannte systematische Messabweichung von X₂ = - 0,06 mm besitzen. Zur Vereinfachung soll zunächst die systematische Unsicherheit von X₂ vernachlässigt werden. Die gesuchte physikalische Größe Y ergibt sich dann durch Y = X₁ – X₂, wobei die Eingangsgröße X₁ die Größe bezeichnet, die sich zunächst bei der Messdatenauswertung ergibt. Die Größe K = - X₂ nennt man Korrektion und es gilt: Y = X₁ + K (Ergebnisgröße ist gleich Eingangsgröße plus Korrektion). Im Beispiel beträgt die Korrektion des Längenmessgerätes K = + 0,06 mm. Messgeräte, besonders in der Präzisionsmesstechnik, sind manchmal mit Korrektionstabellen ausgestattet.

Die geschilderte Vorüberlegung bezüglich der Notwendigkeit einer Korrektion bezeichnet man nach der Terminologie des GUM und der DIN 1319-3 als die "Aufstellung des Modells" zur Bestimmung einer einfachen Messgröße.

(Bei den Messgeräten im Physiklabor ist normalerweise keine Korrektion erforderlich.)

Anmerkungen zum Messverfahren:

Bei einer Längenmessung könnten als Messverfahren zum Beispiel 1. ein einfacher Maßstab, 2. ein Messschieber, 3. eine Präzisionsmessuhr oder 4. ein optisches Laserinterferometer verwendet werden. Die genannten Verfahren sind qualitativ sehr unterschiedlich. Deshalb werden sie wahrscheinlich unterschiedliche Messwerte liefern, wobei nicht ausgeschlossen ist, dass sich zufällig auch gleiche Zahlenwerte ergeben können. Die Streuung der Messdaten (und damit die Messunsicherheit) wird in den Beispielen 1 – 4 aber sehr unterschiedlich sein.

Eine Einzelmessung allein wird im allgemeinen nicht die Messgröße Y ergeben. Vielmehr treten unvermeidbar Messabweichungen zwischen dem Ergebnis einer Einzelmessung v_j und dem wahren Wert der Messgröße Y auf. Man bestimmt deshalb aus den Einzelmessungen v_j einer Messung einen Schätzwert y, wobei y dann als Näherung für die Messgröße Y angesehen wird, . Man geht dabei davon aus, dass Einzelmessungen bedingt durch rein zufällige Einflüsse um den wahren Wert der Messgröße streuen. Verallgemeinernd betrachtet man Messwerte als Realisierung einer Zufallsgröße V, die dann der Eingangsgröße X₁ zugeordnet wird. Die Verteilung der Zufallsgröße folgt einer Wahrscheinlichkeitsverteilung, die a priori nicht bekannt ist und die im Prinzip durch eine (unendlich) große Zahl von Messungen bestimmt werden müsste.

Tabelle 1: Die Einzelmesswerte der Längenmessung (Beispiel A.1 der DIN 1319-3) sowie Zwischenwerte für weitere Berechnungen sind in der folgenden Tabelle zusammengestellt.

Messung Nr. j	Länge vj mm	(vj - vm) mm	(vj - vm)^2 mm^2	vj^2 mm^2
1	150,14	0,12	0,0144	22542,02
2	150,04	0,02	0,0004	22512,00
3	149,97	-0,05	0,0025	22491,00
4	150,08	0,06	0,0036	22524,01
5	149,93	-0,09	0,0081	22479,00
6	149,99	-0,03	0,0009	22497,00
7	150,13	0,11	0,0121	22539,02
8	150,09	0,07	0,0049	22527,01
9	149,89	-0,13	0,0169	22467,01
10	150,01	-0,01	0,0001	22503,00
11	149,99	-0,03	0,0009	22497,00
12	150,04	0,02	0,0004	22512,00
13	150,02	0,00	0,0000	22506,00
14	149,94	-0,08	0,0064	22482,00
15	150,19	0,17	0,0289	22557,04
16	149,93	-0,09	0,0081	22479,00
17	150,09	0,07	0,0049	22527,01
18	149,83	-0,19	0,0361	22449,03
19	150,03	0,01	0,0001	22509,00
20	150,07	0,05	0,0025	22521,00
Summen:	3000,40	0,00	0,1522	450120,16
Mittelwert vm:	150,02

In DIN 1319-3 werden Empfehlungen für das praktische Vorgehen bei einer begrenzten Anzahl von Messungen gegeben: Aus einer Reihe von Einzelmessungen v_j (j = 1,2,3,......n) wird zunächst der Schätzwert x₁ der Eingangsgröße X_i und eine Messunsicherheit u(x₁) bestimmt. Die Einzelmessungen v_j sollen zufällig um die Messgröße Y streuen. Sehr oft kann die Häufigkeitsverteilung der Einzelmessungen durch eine Normalverteilung nach Gauß beschrieben werden. Nach der Wahrscheinlichkeitstheorie erhält man Gauß-Verteilungen bei rein zufälligen Abweichungen zwischen Einzelmessung und Erwartungswert.

Nach den statistischen Gesetzen ist bei einer unendlichen Anzahl von Einzelmessungen v_j ist der Erwartungswert m einer Wahrscheinlichkeitsverteilung der Grenzwert n ® ¥ des arithmetischen Mittels:

(1)

Bei einer endlichen Anzahl von Messungen verwendet man den arithmetischen Mittelwert als Schätzwert für m und definiert ihn deshalb auch als Schätzwert x₁ der Eingangsgröße X₁:

(2)

Die Standardabweichung s (bzw. die Varianz s², das Quadrat der Standardabweichung) wird bei einer unendlichen Anzahl von Messungen in folgender Form definiert:

(3)

Bei einer endlichen Anzahl von Messungen ist aber nicht der Erwartungswert m sondern nur dessen Schätzwert bekannt. Dies führt zur Definition einer (empirischen) Standardabweichung s in der Form:

(4)

Hinweis: Die beiden Ausdrücke in Gleichung (4) sind identisch. Der erste ist zweckmäßig, wenn bereits bekannt ist und anschließend s berechnet werden soll. Der zweite Ausdruck ist vorteilhaft, wenn man die Berechnung von und s mit einem Rechner ausführt möchte, und direkt bei der Eingabe von v_j die Summe der Messwerte S_M und die Summe der Quadrate der Messwerte S_Q addieren kann. Es erspart eine doppelte Eingabe der Messwerte.

Bestätigung für die Identität der Ausdrücke in Gleichung (4):

(5)

Mit und ergibt sich: und (6)

Die (empirische) Standardabweichung s charakterisiert die Abweichung, die Einzelmessungen vom Schätzwert haben können. Da jede endliche Menge von Messwerten aber nur die Realisierungen einer Zufallsgröße darstellt (eine zweite unabhängige Messung liefert sicher andere Messwerte) kann auch vom Erwartungswert m und die empirische Standardabweichung s von der Standardabweichung s der Wahrscheinlichkeitsverteilung abweichen.

Die Standard(mess)unsicherheit u(x₁) ist definiert als die (empirische) Standardabweichung des Mittelwertes :

(7)

2.2 Anwendung der Definitionen am Beispiel Längenmessung

2.2.1 Schätzwert x₁ der Eingangsgröße X₁ als Mittelwert der Messwerte:

(8)

2.2.2 (Empirische) Standardabweichung s der Messwerte:

(9)

(Empirische) Standardabweichung alternativ:

(10)

(Der Unterschied in der letzten Stelle beruht auf Rundungsfehlern.)

2.2.3 Standard(mess)unsicherheit u(x₁) des Schätzwertes:

(11)

Hinweis: Bei der Verwendung von EXCEL stehen für die Berechnung von und s die Funktionen "MITTELWERT" und "STABW" zur Verfügung. Um u(x₁) zu berechnen, muss der mit der STABW-Funktion berechnete Werte durch dividiert werden.

2.3 Darstellung der Messwertverteilung

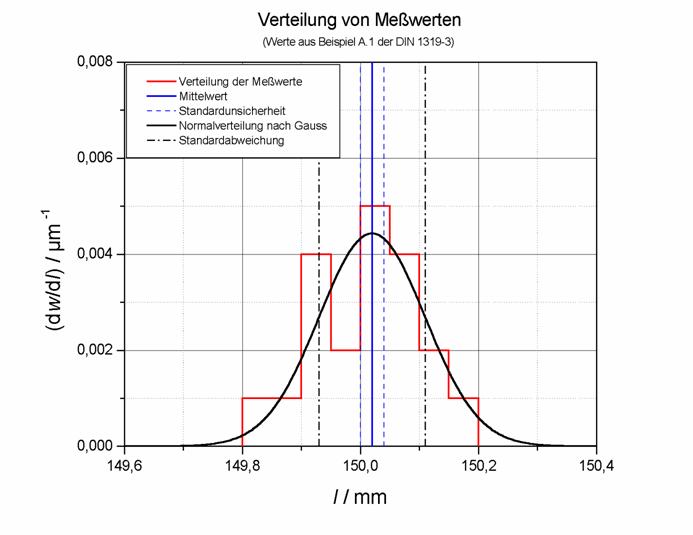
In der Figur 1 wurden die Häufigkeitsverteilung der Messwerte aus Tabelle 1 und die Gaußsche-Normalverteilung graphisch aufgetragen, wobei entsprechend üblicher Konvention, das Integral der Verteilungen auf 1 normiert wurde.

Zur Erläuterung: Die rote Treppenkurve zeigt die Wahrscheinlichkeit pro Längenintervall mit einem . Die Werte wurden über einen Bereich von gemittelt.

Die schwarze glatte Kurve zeigt zum Vergleich die Normalverteilung nach Gauß, wobei der Erwartungswert m durch den Mittelwert der Messwerte und die Standardabweichung s durch die empirische Standardabweichung ersetzt wurden:

(12)

Man erkennt, dass die experimentelle Verteilung recht gut durch die Gaußsche-Normalverteilung beschrieben wird.

Fig. 1. Wahrscheinlichkeitsverteilung der Messwerte pro Längenintervall Dl = 1µm. Die Integrale der Verteilungen sind auf den Wert 1 normiert.

Mittelwert:

Standardunsicherheit des Mittelwertes:

Standardabweichung:

Normalverteilung nach Gauss:

Verteilung der Messwerte gemittelt über eine Intervallbreite von 50 µm.

Normierungvon (dw/dl):

Interpretation: Die (empirische) Standardabweichung s charakterisiert die Streuung der Einzelmessungen in Bezug auf den Schätzwert x₁, ( ~ wahren Messwertes X₁). Alle Messreihen, die mit der selben Messeinrichtung durchgeführt werden, sollten deshalb (bis auf zufällige Abweichungen) ähnliche Werte für s ergeben. Der Wert von s hängt insbesondere nicht von der Anzahl n der Messungen ab (s ändert sich, wenn andere, z. B. ein genauere oder ungenauere Messeinrichtungen gewählt werden). Die Unsicherheit des Mittelwertes, die Standard(mess)unsicherheit, u(x₁) wird kleiner, wenn die Anzahl der Messungen erhöht wird. Allerdings ändert sich u(x₁) nur proportional zu , d. h. man muss viermal so häufig messen, um die Standard(mess)unsicherheit des Mittelwertes zu halbieren.

2.4 Relative Unsicherheit, erweiterte Unsicherheit, Vertrauensbereich

Relative Messunsicherheit: Unter der relativen Messunsicherheit versteht man:

, (13)

wenn ist. Der Wert von ist also immer positiv und wird oft in Prozent oder Promille angegeben.

Erweiterte Messunsicherheit: Bei Messwertverteilung, die durch eine Gaußsche-Normalverteilung mit den Parametern µ und s beschrieben werden kann, beträgt die Wahrscheinlichkeit, dass das Ergebnis einer zusätzlichen Einzelmessung innerhalb des Intervalls liegt, 66%. Bei einer endlichen (aber sehr großen!) Anzahl von Messungen gilt dies näherungsweise auch für das aus den Schätzwerten gebildete Intervall . Die Standardabweichung des Mittelwerte hat folgende Bedeutung: Jede weitere Messreihe mit einer vergleichbaren Anzahl von Einzelmessungen ergibt als einen neuen Schätzwert ( = Mittelwert der zusätzlichen Messreihe). Die Werte liegen mit einer Wahrscheinlichkeit von 66% innerhalb des Intervalls . Es folgt, dass auch der (unbekannten) wahren Wert der Messgröße mit entsprechender Wahrscheinlichkeit in diesem Intervall liegen muss. Bei vielen praktischen Messproblemen, z. B. industriellen Kontrollprozessen oder der Angabe von Prüfergebnissen, bevorzugt man größere Intervallbreiten, die dann den wahren Wert mit einer größeren Wahrscheinlichkeit als 66% enthalten. In der DIN 1319 wird hierfür die Verwendung eines Erweiterungsfaktors k empfohlen, der das Intervall definiert. Man kann unter Annahme einer Gauß-Verteilung und Vorgabe einer beliebigen Wahrscheinlichkeit P (0% < P < 100%) mit der den wahren Wert enthalten soll, den entsprechenden Faktor k berechnen. Von besonderer praktischer Bedeutung ist der Erweiterungsfaktor k = 2. Das Intervall enthält den wahren Wert mit einer Wahrscheinlichkeit von 95%.

Hinweis: Verwendet man k > 1,also z. B. k = 2, so nennt man die „mit dem Erweiterungsfaktor k (z. B. zwei) versehenen Standard(mess)unsicherheit“.

(In der früherer Nomenklatur entsprach dies einem „zwei Sigma-Fehler“.)

Vertrauensbereiche: Die angegeben Wahrscheinlichkeitswerte von 66% für k = 1 bzw. 95% für k = 2 gelten exakt nur Vorliegen der durch die Parameter µ und s beschriebene Gaußschen-Normalverteilung. Die Parameter µ und s sind aber, wie oben diskutiert, üblicherweise nicht bekannt sind, sondern werden durch und abgeschätzt, wobei und s mit Hilfe der Gleichungen (2), (4) empirisch aus den Einzelmesswerten bestimmt werden. Die Schätzungen besitzen Unsicherheiten, die umso größer sind, je weniger Einzelmessungen vorliegen. Formal kann man und s (und damit auch u(x₁)) schon aus zwei Einzelmessungen berechnen, aber die Schätzungen und werden bei sonst gleichen Bedingungen genauer sein, wenn mehr Einzelmessungen vorliegen. Die bisherigen Angaben über die Wahrscheinlichkeit den wahren Wert in einem durch und s oder und k×s gegebenem Intervall zu finden, gelten nur für viele ("unendlich viele") Einzelmessungen. Bei einer endlichen Anzahl n von Einzelmessungen ist eine Korrektur erforderlich.

t-Faktor Korrektur: Nach DIN 1319-3 kann mit Hilfe eines Korrektionsfaktors t, der auf der Basis der Student- oder t-Verteilung bei einer endlichen Anzahl von n = 2,3.... Einzelmessungen und Vorgabe eines bestimmten Vertrauensniveaus (z. B. 95%) berechnet werden kann, das Vertrauensintervalls angeben werden. Für ein 95% Vertrauensniveau sind einige t-Faktoren in der folgenden Tabelle 2 aufgeführt. Es zeigt sich, dass für praktische Zwecke schon n > 10 als ausreichend große Anzahl angesehen werden kann.

Tabelle 2: t-Faktoren für ein Vertrauensniveau von 95%

n =	2	3	4	5	6	7	8	9	10	12	20	30	50	100
t =	12,71	4,30	3,18	2,78	2,57	2,45	2,36	2,31	2,26	2,20	2,09	2,05	2,01	1,98

Hinweis: Man beachte die unterschiedliche Bedeutung des Erweiterungsfaktors k und des Korrektionsfaktors t.

· k bezeichnet eine Erweiterung der Standard(mess)unsicherheit und kann unabhängig von der Anzahl der Einzelmessungen vom Anwender definiert werden. Man muss immer den Wert von k zusammen mit der erweiterten Messunsicherheit angeben.

· t ist ein beim Vorliegen bestimmter Voraussetzungen (Gaußsche Normalverteilung der Zufallsvariablen) ein auf die Standard(mess)unsicherheit anzuwendender Faktor, der bei endlicher Anzahl von Einzelmessungen und Vorgabe des Vertrauensniveaus die wahre Größe des Vertrauensintervall ergibt. Der t-Faktor kann der Tabelle 1 der DIN 1319-3 (oder obigem Auszug) entnommen werden. Im Zusammenhang mit der Angabe eines Vertrauensintervall muss immer das Vertrauensniveau angegeben werden. Eine Angabe des t-Faktors ist entbehrlich.

Beispiel Längenmessung: Der Schätzwert der Eingangsgröße betrug . Die (empirische) Standardabweichung und die Standard(mess)unsicherheit des Mittelwertes . Die Ergebnisgröße y erhält man durch Anwendung der Korrektion : . Die relative Messunsicherheit beträgt: . Die mit dem Erweiterungsfaktor k = 2 versehen Messunsicherheit ist . Bei 20 Messwerten und einem Vertrauensniveau von 95% ist der t-Faktor 2,09 (siehe Tabelle 2), so dass ergibt. Die Vertrauensgrenzen für das Vertrauensniveau von 95% sind und .

2.5 Das vollständige Messergebnis

Das vollständige Messergebnis soll nach DIN 1319-3 in einer der folgenden Schreibweisen angegeben werden:

1. Beispiel: 150,08 mm, 0,02 mm

2. Beispiel: 150,08 mm, 0,014%

3. Y = y (u(y)) Beispiel: L = 150,08 mm (0,02 mm)

4. Beispiel: L = (150,08 mm ± 0,02 mm) = (150,08 ± 0,02) mm

5. Beispiel: L = 150,08 mm (1 ± 1,4 10^-4)

Hinweis: In Versuchsprotokollen kann eine dieser empfohlen Schreibweisen verwendet werden. Sie sollte im gesamten Protokoll einheitlich sein. Eigenkreationen sind nicht sinnvoll. Falls Sie einen Erweiterungsfaktor k verwenden, empfiehlt es sich, diesen erst zum Schluss, d. h. bei der Angabe des Endergebnisses einer Messgröße zu verwenden. Riskant ist es, wenn bei verschiedenen Eingangsgrößen unterschiedliche Erweiterungsfaktoren verwendet werden. Bei der Bestimmung der Gesamtunsicherheit einer Ergenisgröße (siehe unten) dürfen nämlich nur die Standard(mess)unsichheiten der Eingangsgrößen verwendet werden.

Einschränkungen: Die beschriebe Bestimmung der Standardabweichung aus Messwerten ist nicht immer sinnvoll. Hat man zum Beispiel eine sehr gut bekannte Messeinrichtung (z. B. bei einer industrielle Prozesskontrolle), deren Standardabweichung s₀ aus einer Vielzahl von Vormessungen bekannt ist, dann empfiehlt die DIN 1319-3 diese zu verwenden und die Standard(mess)unsicherheit einer Stichprobe wie folgt zu berechnen .

Vorüberlegungen: Es empfiehlt sich, schon vor und während der Durchführung einer Messung die Auswirkungen auf die Messunsicherheit zu berücksichtigen. Bei der Festlegung der Anzahl der Einzelmessungen empfiehlt sich ein Kompromiss im Hinblick Messaufwand und angestrebter Genauigkeit. Bei einer sehr kleinen Zahl von Messungen ist der t-Faktor, der bei der Angabe des Vertrauensintervalls benötigt wird, sehr groß. Er beträgt für das Vertrauensniveau von 95% z. B. bei zwei Einzelmessungen 12,7. Einige weitere Messungen, z. B. schon fünf oder sechs genügen, um einen deutlich kleineren t-Faktor von ~ 2 zu erhalten. Falsch ist es (aber gelegentlich in Versuchsprotokollen zu finden und besonders bei wenigen Messwerten auffällig) statt der Unsicherheiten oder den Vertrauensbereich anzugeben.

2.6 Systematische Unsicherheiten

Systematische Unsicherheiten: Die systematische Messabweichung besteht nach der Terminologie der DIN-1319 aus einem bekannten und aus einem unbekannten Anteil. Die bekannte systematische Messabweichung führt zu einer Korrektion K, die im allgemeinen auch eine gewisse Untersicherheit besitzt. Diese Unsicherheit ist auch dann vorhanden, wenn K = 0 ist. Die Unsicherheit der Korrektion entspricht einer unbekannten systematischen Unsicherheit. Im Beispiel Längenmessung wurde sie zur Vereinfachung vernachlässigt. Auch in den Versuchen des Physiklabors kann man in sehr vielen Fällen auf die Berücksichtigung unbekannter systematischer Unsicherheiten verzichten (nicht zuletzt, weil man sie, der Name sagt es, nicht oder nur schwer quantifiziert werden können). Allerdings sollte man dann, wenn keine zufällige Messabweichung vorliegt (z. B. bei Verwendung von Messgeräten mit Digitalanzeige, oder im Versuch "Dichtebestimmung mit der Mohrschen Waage") den Einfluss systematischer Unsicherheiten in Betracht ziehen. Es existiert kein allgemeingültiges Konzept, aber einfache Abschätzungen können nützlich sein. Führt eine systematische Messabweichung, über deren Ursache nichts weiter bekannt sein muss, zu den Messwerten a oder b (z. B. wenn die letzte Stelle einer Digitalanzeige zwischen zwei Ziffern hin und her springt, oder wenn die Mohrsche Waage bei zwei benachbarten Drehmomenteinstellung "fast" Gleichgewicht anzeigt) so sollte nach Empfehlung der DIN Norm die systematische Abweichung nach:

(13)

berechnet werden und als deren Unsicherheit

(14)

verwendet werden. Die Unsicherheit der Ergebnisgröße errechnet sich dann nach der Beziehung:

. (15)

3. Auswertungsverfahren bei mehreren Eingangsgrößen

3.1 Korrelationen

In vielen Fällen muss man zur Bestimmung einer physikalischen Größe zunächst mehrere Eingangsgrößen messen, aus denen anschließend bei der Auswertung die gesuchte Größe, die Ergebnisgröße, berechnet wird.

Beispiele:

Rechteckfläche: Zur Bestimmung einer Rechteckfläche wird im allgemeinen nicht die Fläche direkt, sondern zunächst die Länge der beiden Seiten a und b gemessen. Die Fläche ergibt sich als Produkt .

Umfang: Zur Bestimmung des Umfangs U des Rechtecks kann man ebenfalls zunächst die Seitenlängen a und b messen und U durch berechnen.

Eigen(kreis)frequenz: Die Eigen(kreis)frequenz w₀ eines ungedämpften Drehpendels kann aus dem Massenträgheitsmoment J und der Winkelrichtgröße D^* mit Hilfe der Beziehung berechnet werden.

In DIN 1319-3 wird das Auswerteverfahren für den allgemeinen Fall sehr ausführlich (aber sehr abstrakt) behandelt. Das Verfahren ist mathematisch aufwendig, weil man im allgemeinen sowohl korrelierte als auch unkorrelierte Beträge berücksichtigen muss, wie in den folgenden Beispielen verdeutlicht wird:

Bei der Messung der Seitenlängen a und b mit Hilfe einer Messeinrichtung (z. B. Vergleichsmaßstab) treten jeweils zufällige Messabweichungen auf, aus denen nach dem oben beschriebenen Verfahren die (zufälligen) Unsicherheiten u(a) und u(b) berechnet werden. Die zufälligen Abweichungen der Einzelmessungen sind unabhängig voneinander. Man nennt sie deshalb unkorreliert. Verwendet man aber bei den Messungen von a und b aber die selbe Messeinrichtung mit einer systematischen Unsicherheit (die z. B. einer Kalibrierunsicherheit des Maßstabes entspricht) dann sind die systematischen Unsicherheitsbeiträge als korreliert zu betrachten. Im allgemeinen hat man also als Eingangsdaten sowohl mit korrelierter als auch unkorrelierter Unsicherheitsbeiträgen vorliegen, die man dann mathematisch korrekt zur Gesamtunsicherheit der Ergebnisgröße zusammenfassen muss.

Vorüberlegungen an einem Beispiel: Zur Bestimmung der Eigen(kreis)frequenz eines Drehpendels im Physiklabor ermittelt man die Winkelrichtgröße D* und das Massenträgheitsmoment J in unabhängigen Messungen. Zunächst wird mit einem Federkraftmesser die Kraft F zur Erzeugung eines Drehmoments M an einem Hebelarm l gemessen, berechnet, und dann die Winkelrichtgröße D^* als Quotient aus Drehmoment M und der beobachteten Winkelauslenkung j durch bestimmt. Das Trägheitsmoment J hängt von der Verteilung der Massenelemente des Körpers bezüglich der Drehachse ab. Bei einer Scheibe mit Radius R und Gesamtmasse m gilt bezüglich einer Drehachse, die durch den Scheibenmittelpunkt geht und senkrecht auf der Scheibe steht, . Die Bestimmungen von Massenträgheitsmoment J und Winkelrichtgröße D^* basieren also auf Wägung, Längenmessung, Kraftmessung und Winkelmessung. Hinsichtlich der Anteile von korrelierten und unkorrelierten Unsicherheitskomponenten zeigt eine Vorüberlegung: Die Messverfahren sind so unterschiedlich, dass sie in guter Näherung als voneinander unabhängig, also als unkorreliert, betrachtet werden können. Korrelierten Anteile in der Unsicherheit von können vernachlässigt werden.

Anmerkung: Bei Vorüberlegungen bezüglich korrelierter und unkorrelierter Anteile muss natürlich immer der angestrebte Genauigkeitsgrad berücksichtigt werden, bevor begründete Entscheidungen über eine Vernachlässigungen getroffen werden können. Im vorliegenden Beispiel könnten durchaus Korrelationen zwischen der Längenmessung des Hebelarms (Bestimmung von M und dann D^*) und der des Scheibendurchmessers (Bestimmung von J) vorliegen.

Unter der Vorraussetzung, dass eine Gesamtmessunsicherheit nur unkorrelierte Anteile enthält, ergeben sich erhebliche mathematische Vereinfachungen. Die "praktische Erfahrung" zeigt, dass selbst dann, wenn Korrelationen vorhanden sind, der Einfluss auf die Gesamtunsicherheit des Endergebnisses normalerweise klein ist. Bei den Versuchen im Physiklabor, kann man deshalb die Unsicherheiten der Ergebnisgröße immer unter der Annahme vollständig unkorrelierter Eingangsgrößen berechnen.

3.2 Allgemeines Verfahren

Nach DIN 1319-3 besteht der erste Schritt jedes Auswertungsverfahrens in der Aufstellung eines Modells, das den mathematischen Zusammenhang zwischen den Eingangsgrößen und der Ergebnisgrößen enthält. In den oben genannten Beispielen sind Rechteckfläche F, Umfang U und Eigenfrequenz w₀ die Ergebnisgrößen, die Seiten a und b, die Winkelrichtgröße D* und das Massenträgheitsmoment J die Eingangsgrößen und die Beziehungen , und stellen die Modelle dar.

In einer mathematischen Terminologie kann eine Ergebnisgröße Y bzw. deren Schätzwert y als Funktion f der Variablen x_i, i = 1,............m beschrieben werden:

(16)

wobei X₁, X₂, ....X_m die Eingangsgrößen, x₁, x₂,...x_m die entsprechenden Schätzwerte der Eingangsgrößen darstellen.

Für die Unsicherheit der Ergebnisgröße gilt (hier: die allgemeine Gleichung für korrelierte und unkorrelierte Eingangsgrößen):

(17)

wobei und die partiellen Ableitungen der Funktion f nach den Variablen x_i und x_k sind und u(x_i,x_k) die den Variablen x_i und x_k zugeordnete Unsicherheitskomponente darstellt. Die Komponenten u(x_i,x_k) können sowohl korrelierte als auch unkorrelierte Unsicherheitsbeiträge enthalten.

Anmerkung: Die Menge der u(x_i,x_k) Komponenten stellt eine symmetrische Matrix mit Zeilen und Spalten dar (Unsicherheitsmatrix). Die Komponenten u(x_i,x_k) können als Produkt aus den individuellen Unsicherheiten u(x_i) und u(x_k) und einem Korrelationskoeffizienten r(x_i,x_k) ausgedrückt werden: . Die r(x_i,x_k) Werte liegen zwischen 0 und 1. Sie beschreiben die Wahrscheinlichkeit, mit der die Eingangsgrößen x_i mit der Eingangsgröße x_k korreliert ist, wobei der Wert 0 bei vollständig unkorrelierten und der Wert 1 bei vollständig korrelierten Eingangsgrößen angenommen wird. Aus der Definition folgt deshalb unmittelbar, dass (der Korrelationskoeffzient bleibt beim Vertauschen der Variablen gleich) und (eine Variable ist mit sich selbst immer maximal korreliert) gilt. Die Korrelationskoeffizienten bilden die Korrelationsmatrix, die ebenfalls aus m Zeilen und m Spalten gebildet wird, und wegen der Nebenbedingung spiegelsymmetrisch ist. Die Elemente in der Hauptdiagonalen haben immer den Wert 1. In der Hauptdiagonalen der Unsicherheitsmatrix stehen deshalb die Quadrate der Unsicherheiten der Eingangsgrößen. Diese werden durch , d. h. durch die empirischen Varianzen abgeschätzt. Die Komponenten u(x_i,x_k) mit , also alle Matrixelemente, die nicht auf der Hauptdiagonalen stehen, nennt man Kovarianzen. Die vollständige Aufstellung der Unsicherheitsmatrix im Fall einer vorhandener Korrelationen zwischen den Eingangsgrößen ist schwierig und erfordert z. B. Kenntnis oder Annahmen über die Korrelationskoeffizienten . Wenn alle Eingangsgrößen dagegen unkorreliert sind, vereinfacht sich die Berechnung der Unsicherheit erheblich, da dann alle Kovarianzen verschwinden und nur noch die Varianzen übrig bleiben..

3.3 Verfahren bei unkorrelierten Eingangsgrößen

Bei unkorrelierten Eingangsgrößen wird das Quadrat der Unsicherheit der Ergebnisgröße durch die folgende Gleichung gegeben:

(18)

Gleichung (18) stellt die Grundgleichung für die Ermittlung von Gesamtunsicherheiten dar, sofern die Eingangsgrößen als unkorreliert betrachtet werden können (z. B. im Physiklabor), und ist für alle Modellfunktionen f anwendbar, sofern diese differenzierbar sind. Zunächst sollen die Unsicherheiten der Ergebnisgrößen in den Beispielen: Flächen- Umfang und Kreisfrequenzbestimmung mit Hilfe der Beziehung (18) ermittelt werden. Die Berechnung kann im Einzelfall umfangreich sein. Deshalb werden im Abschnitt 3.4. einige einfache Regeln vorgestellt, die es gestatten, für den größten Teil der in der Praxis relevanten Modellfunktionen Unsicherheitsberechnungen stark zu vereinfachen.

Berechnung von Gesamtunsicherheiten mit Hilfe der Gleichung (18):

Beispiel Flächenbestimmung: Das Modell lautet: . Durch Längenmessung der Seitenlängen und wird die Unsicherheit der Eingangsgrößen, u(a) und u(b), bestimmt. Nach Gleichung (19) ist das Quadrat der Standard(mess)unsicherheit der Fläche F gleich:

(19)

Beispiel Umfangsbestimmung: Das Modell lautet: . Die u(a) und u(b) sollen wieder die Standard(mess)unsicherheiten der Eingangsgrößen sein. Nach Gleichung (19) ist das Quadrat der Standard(mess)unsicherheit des Umfangs U gleich:

(20)

Beispiel Eigen(kreis)frequenzbestimmung: Das Modell lautet: . Die u(D^*) und u(J) sind die Standard(mess)unsicherheiten der Eingangsgrößen.

(21)

Das letzten Beispiel zeigt, dass die direkte Berechnungen mit Hilfe der Gleichung (18) umfangreich sein kann. Man kann aber mit Hilfe einiger einfacher Regeln für sehr viele Modellfunktion die Unsicherheit der Ergebnisgröße erheblich einfacher bestimmen:

3.4 Regeln zur Vereinfachung der Unsicherheitsermittlung

Regel 1 Ist die Ergebnisgröße eine Summe von m Eingangsgrößen, so ist das Quadrat der Unsicherheit von f die Summe der Quadrate der Unsicherheiten der Eingangsgrößen x_i.

(22)

Beweis: Bei partiellen Ableitungen nach x_i werden alle Variablen x_j als konstant angesehen. Es gilt also:

(23)

(24)

Regel 2 Ist die Ergebnisgröße eine Summe von m Eingangsgrößen mit den konstanten Koeffizienten a_i, so ist das Quadrat der Unsicherheit von f die Summe der Quadrate der Unsicherheiten der Eingangsgrößen multipliziert mit .

(25)

Beweis: Analog zum Beweis 1 gilt:

(26)

(27)

Regel 3 Ist die Ergebnisgröße die Differenz zweier Eingangsgrößen x₁ und x₂ mit den konstanten Koeffizienten a₁ und a₂, , so ist das Quadrat der Unsicherheit von f die Summe der Quadrate der Unsicherheiten der Eingangsgrößen multipliziert mit .

(28)

Beweis: Es gilt: . Wenden Sie Regel 2 an.

Regel 4 Ist die Ergebnisgröße ein Produkt von m Eingangsgrößen x_i, so ist das Quadrat der relativen Unsicherheit von f, ,die Summe der Quadrate der relativen Unsicherheiten der Eingangsgrößen .

(29)

Beweis: Bei einer partiellen Ableitung nach x_i werden alle Variablen x_j als konstant angesehen. Es gilt also:

(30)

und es folgt:

(31)

Regel 5 Ist die Ergebnisgröße die k-te Potenz der Eingangsgröße x₁, dann ist die relative Unsicherheit von f gleich dem Produkt von k und der relativen Unsicherheit von x₁.

(32)

Beweis:

(33)

Regel 6 Ist die Ergebnisgröße f der Quotient der Eingangsgrößen x₁ und x₂, , dann ist das Quadrat der relativen Unsicherheit von f gleich der Summe der relative Unsicherheiten der Eingangsgrößen x₁ und x_2.

(34)

Beweis: Man schreibe f in der Form: und wende Regel 4 und Regel 5 an.

Regel 7 Ist die Ergebnisgröße eine Exponentialfunktion mit der Eingangsgröße x₁ im Exponenten, ,dann ist die relative Unsicherheit von f gleich der (absoluten) Unsicherheit der Eingangsgröße x₁.

(35)

Beweis:

(36)

3.5 Anwendungsbeispiele

Flächenbestimmung: Die Modellfunktion lautet: . Mit Regel 4 folgt direkt:

(37)

Umfangsbestimmung: Die Modellfunktion lautet: . Mit Regel 2 folgt:

(38)

Bestimmung der Eigen(kreis)frequenz: Die Modellfunktion für (unter Verwendung des Tragheitsmomentes einer Scheibe) verwendet lautet:

. Mit Regel 4 und Regel 5 folgt:

(39)

Weiter Beispiele: Die Modellfunktion soll lauten: . Man ersetze zunächst den Nenner durch :

(40)

Es folgt nach Regel 5 und Regel 6:

(41)

Mit Regel 2 erhält man:

(42)

und durch Kombination von (41) und (42):

(43)

4. Zusammenfassung:

1. Besteht eine Messreihe aus mehr als einer Einzelmessung, so ermittele man den Schätzwert x₁ der Eingangsgröße X₁ als arithmetisches Mittel der Einzelmessungen v_j:

2. Man berechne die Standard(mess)unsicherheit u(x₁) mit Hilfe der Beziehung:

3. Prüfen Sie, ob die Eingangsgröße einer Korrektion bedarf und berechnen Sie die Ergebnisgröße y durch:

4. Kann eine systematische Unsicherheit u(x₂) angegeben und abgeschätzt werden, ergibt sich die Unsicherheit der Ergebnisgröße durch:

5. Geben Sie für alle im Versuch gemessenen Größen den Messwert zusammen mit der Messunsicherheit an. Verwenden Sie (nur) eine der folgenden Schreibweisen:

1. Beispiel: 150,08 mm, 0,02 mm

2. Beispiel: 150,08 mm, 0,014%

3. Y = y (u(y)) Beispiel: L = 150,08 mm (0,02 mm)

4. Beispiel: L = (150,08 mm ± 0,02 mm) =

= (150,08 ± 0,02) mm

5. Beispiel: L = 150,08 mm (1 ± 1,4 10^-4)

Die Messunsicherheit kann entweder als Standard(mess)unsicherheit u(y) oder als eine mit einem Erweiterungsfaktor k > 1 versehen erweiterte Messunsicherheit angegeben werde. Falls keine Angaben über die Messunsicherheit gemacht werden, muss die Standard(mess)unsicherheit angegeben werden. Verwenden Sie einen Erweiterungsfaktor k, so muss dieser benannt werden.

6. Man prüfe, ob die zusätzliche Angabe eines Vertrauensintervalls sinnvoll ist. Berechnen Sie das Vertrauensintervall zu einem von Ihnen gewählten Vertrauensniveau (Empfehlung: 95%) mit Hilfe eines t-Faktors und geben Sie das Vertrauensintervall immer zusammen mit dem Vertrauensniveau an.

7. Falls eine Ergebnisgröße y aus mehreren Einzelmessgrößen x₁, x₂,..........x_m zusammengesetzt ist, stellen Sie möglichst schon vor Messbeginn die Modellfunktion auf. Überlegen Sie anhand der Modellfunktion die Anforderungen bezüglich der Genauigkeit der verschiedenen Einzelgrößen. Berechnen Sie bei der Auswertung die Unsicherheit der Ergebnisgröße unter der vereinfachten Annahme unkorrelierter Eingangsgrößen nach der Beziehung:

oder verwenden Sie (falls möglich) die in Abschnitt 3.3. beschriebenen Regeln.

8. Die Begriffe Mittelwert, Standard(mess)unsicherheit, Abweichung, erweiterte Unsicherheit, Vertrauensintervall, Vertrauensniveau, Vertrauensgrenzen dürfen nur mit den in der DIN 1391-3 gegebenen Definitionen verwendet werden. Eine Wiederholung der Definitionsgleichungen im Versuchsprotokoll ist überflüssig. (Sollten Sie ältere Versuchsprotokolle als "Vorlage" verwenden, achten Sie daraus, dass in ihrem Protokoll die aktuellen Bezeichnungen gefordert sind.)